Parcial 3
Variante 15
1. La tabla contiene muestras de la señal de velocidad angular ω(t) a la salida de un giroscopio en el intervalo de un segundo 0 ≤ t ≤ 1. Calcule el ángulo de rotación 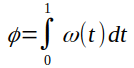 en un segundo utilizando la fórmula de rectángulo, de trapecio y la formula de Simpson.
en un segundo utilizando la fórmula de rectángulo, de trapecio y la formula de Simpson.
| Time |
Value |
| 0 |
1.9 |
| 0.1 |
5.7 |
| 0.2 |
2.3 |
| 0.3 |
2.8 |
| 0.4 |
10.3 |
| 0.5 |
10.4 |
| 0.6 |
1.1 |
| 0.7 |
7.9 |
| 0.8 |
2.9 |
| 0.9 |
3.5 |
| 1 |
8.9 |
2. Calcule el valor de π utilizando el método de Montecarlo. Use 10 mil intentos.
3. Dibuje la gráfica de la función z=sin(x+5)*exp(-(x+5)^2-(y+5)^2). Encuentre el mínimo de la función usando el método de gradiente. Se puede utilizar la diferenciación numérica.
4. Dibuje la gráfica de la función z=-(x+4)^2-(y+3)^2+3. Encuentre el máximo de la función usando el método de Newton.
5. Dibuje la gráfica de la función y=-0.1*(x+1)^2+sin(x). Elija un método de optimización. Encuentra el máximo de la función.
7. Resuelva el problema de valor inicial 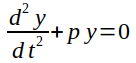 , donde p=-1 con valores iniciales y(0) = +2 y y'(0) = -3 en el intervalo 0 ≤ t ≤ 3 con el método de Euler y el método Heun. Utilice el paso en el tiempo h= 0.1 segundos. Dibuje ambas soluciones en la misma gráfica.
, donde p=-1 con valores iniciales y(0) = +2 y y'(0) = -3 en el intervalo 0 ≤ t ≤ 3 con el método de Euler y el método Heun. Utilice el paso en el tiempo h= 0.1 segundos. Dibuje ambas soluciones en la misma gráfica.
8. Por el método de diferencias finitas, encuentre una solución numérica de la ecuación del enfriamiento de Newton 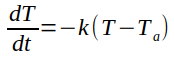 en el intervalo 0 ≤ t ≤ tfin, donde tfin = 2 horas con un paso en el tiempo h = 0.5 horas, k=0.01, temperatura ambiente ta=20°C, y condiciones de fronteras
en el intervalo 0 ≤ t ≤ tfin, donde tfin = 2 horas con un paso en el tiempo h = 0.5 horas, k=0.01, temperatura ambiente ta=20°C, y condiciones de fronteras
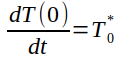 , T(tfin)=Tfin, donde Tfin=27 y T*0=2.5
, T(tfin)=Tfin, donde Tfin=27 y T*0=2.5
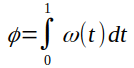 en un segundo utilizando la fórmula de rectángulo, de trapecio y la formula de Simpson.
en un segundo utilizando la fórmula de rectángulo, de trapecio y la formula de Simpson.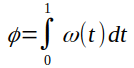 en un segundo utilizando la fórmula de rectángulo, de trapecio y la formula de Simpson.
en un segundo utilizando la fórmula de rectángulo, de trapecio y la formula de Simpson.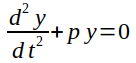 , donde p=-1 con valores iniciales y(0) = +2 y y'(0) = -3 en el intervalo 0 ≤ t ≤ 3 con el método de Euler y el método Heun. Utilice el paso en el tiempo h= 0.1 segundos. Dibuje ambas soluciones en la misma gráfica.
, donde p=-1 con valores iniciales y(0) = +2 y y'(0) = -3 en el intervalo 0 ≤ t ≤ 3 con el método de Euler y el método Heun. Utilice el paso en el tiempo h= 0.1 segundos. Dibuje ambas soluciones en la misma gráfica.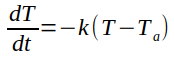 en el intervalo 0 ≤ t ≤ tfin, donde tfin = 2 horas con un paso en el tiempo h = 0.5 horas, k=0.01, temperatura ambiente ta=20°C, y condiciones de fronteras
en el intervalo 0 ≤ t ≤ tfin, donde tfin = 2 horas con un paso en el tiempo h = 0.5 horas, k=0.01, temperatura ambiente ta=20°C, y condiciones de fronteras
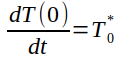 , T(tfin)=Tfin, donde Tfin=27 y T*0=2.5
, T(tfin)=Tfin, donde Tfin=27 y T*0=2.5